Sudoku Swordfish strategy explained

The Sudoku Swordfish strategy is a basic advanced technique applied in the hardest levels of these puzzles to eliminate candidates. It is considered basic due to the clarity of the fish pattern required for its application and its recurrence.
 
The use of this strategy usually results in the unveiling of the solution for one or several cells. It can also allow the player to apply more basic and easier strategies to progress in the puzzle.
 
The grid needs to meet basic constraints in order to apply the Swordfish strategy. When one single constraint is missing, the Finned Swordfish or Sashimi Swordfish variants may apply. In these cases, the elimination of candidates is more restricted but still possible.
 

Requirements to apply the Sudoku Swordfish strategy

The Sudoku Swordfish strategy is a single-candidate technique that uses 3 rows and 3 columns. This means the player only needs to focus on one digit.
 
The grid must contain 3 rows or 3 columns where the digit is a candidate for only 2 or 3 cells. Each cell must be connected to another by row/column, regardless of the shape created when they are linked.
 
Since the digit only has 2 or 3 possible positions in those rows/columns and the cells are linked, it means the solution for that number will forcibly lie within that chain. The player can then test the different possibilities. The digit can then be safely deleted from all the cells where it becomes impossible in all instances.
 
This is the theory, but there is good news! There is no need to test the possibilities because the result is always the same. In every case, the digit cannot be a candidate for any other cell in the same row/column of the connected cells.

Row pattern

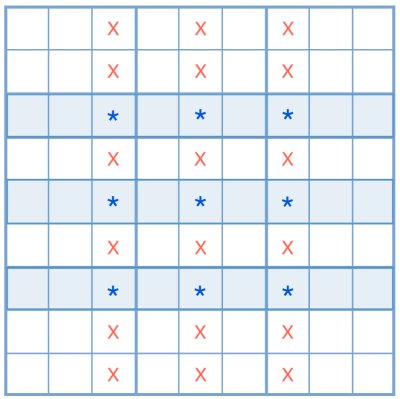
This is the basic configuration needed to be able to apply the Sudoku Swordfish strategy to rows. In the 3 highlighted rows, the digit is only a candidate for three positions. Each position is connected to another by column.
 
The solution for the digit in each of the highlighted rows ensures that it cannot be present in any other position within the columns shared by the cells, regardless of the final configuration of the grid.
 
This basic configuration is the least recurrent in puzzles. To find the necessary pattern in a regular game, the player must ensure that:
- The digit is restricted to 2 or 3 cells in a row.
- Each cell is connected to another by column.
- Each column contains at least 2 shared cells. It is not required that each column contains three cells from the three rows.

Practical example

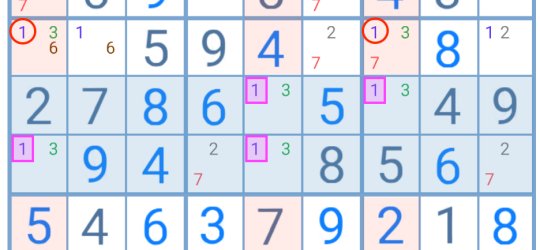
This grid offers a better example of a pattern the player may find when playing a real puzzle.
 
In the three rows highlighted in blue, number 1 has only two possible positions. Since each cell is connected by column, the player has the right pattern to apply the Swordfish technique.
 
As a result, number 1 cannot be a candidate in any other cell in the columns highlighted in red. The player can remove the digits circled in red.

Column pattern

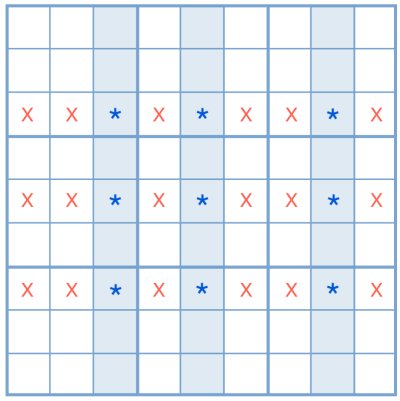
The column pattern follows the exact same principles as the row pattern, but inverted.
 
The digit must be a candidate for only two or three cells in three different columns. Each cell must be connected to at least another by row.
 
By applying the Sudoku Swordfish strategy, the player can thus eliminate that digit as a candidate for any other cells within the shared rows.

Practical example

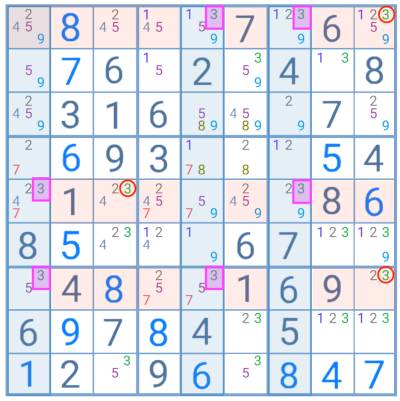
In this practical example, number 3 is a candidate for only 2 cells within the columns highlighted in blue. As each cell is connected to at least another column by row, the player can use the Swordfish technique.
 
Thus, number 3 cannot be a candidate in any cell within the rows highlighted in red. The digits circled in red can be eliminated.

Finned Swordfish Strategy

In this variant, the player finds the digit is a candidate for an extra cell in one of the rows or columns.
 
For example, if the player is looking for a configuration of 2/2/2, it means the digit is a candidate for 3 cells in one of those columns/rows. If the pattern is 3/3/3, then one row/column will have 4 cells with the digit.
 
To apply this strategy, the extra cell must lie within the chain of the Swordfish and share a group with one of the connected cells. It is a fin because it sticks out of the regular fish pattern.
 
Then, the player must answer two key questions. If the fin is false and the Swordfish applies, which candidates can I eliminate? If the fin is true, which candidates are impossible?
 
The candidates that would be impossible when answering both questions, can be safely removed.

Practical example

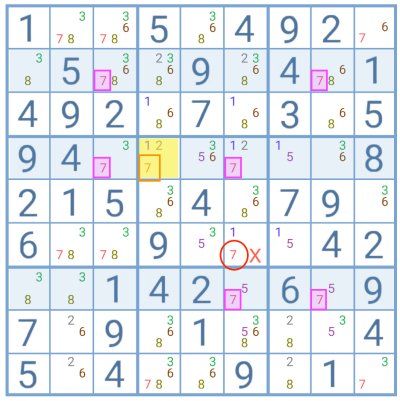
In this example, the 7 in the cell highlighted in yellow invalidates the application of the Sudoku Swordfish strategy to the rows highlighted in blue.
 
However, it lies within the chain of a possible Swordfish and shares the group with one of the cells of this supposed fish pattern. The player can thus apply the Finned Swordfish strategy.
 
Questions: If the Swordfish created by the 7s highlighted in pink applies, which candidates can I eliminate? If the solution for the yellow cell is 7 (and thus there is no Swordfish pattern on the grid) which candidates would it eliminate?
 
The 7 circled in red is the only elimination shared by the answers to those two questions. It can be safely removed.

Sashimi Swordfish

The Sashimi Swordfish requires the presence of fins on the grid. This strategy can only be applied to sets of 2 digits per row or column.
 
Contrary to the Finned technique, the player is now one cell short of finding the pattern to apply the Sudoku Swordfish strategy. Only candidates within the odd-out cell can be eliminated with this technique.
 
It is a rare configuration and, therefore, a technique seldom used. It is, however, very easy to understand with a practical example.

Practical example and explanation

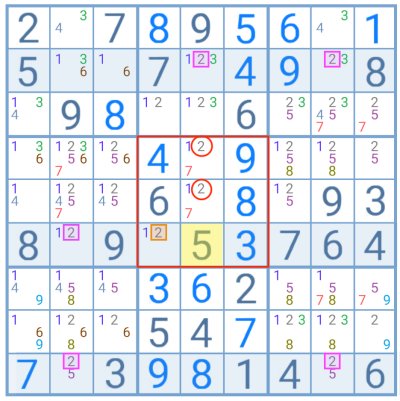
Here the player has three rows where number 2 is a candidate for only two cells. Yet, one of the cells in the second row is not connected to any other cell by column. The Sudoku Swordfish strategy does not apply. To do so, the cell highlighted in yellow (with number 5) would have to contain number 2 as a candidate.
 
The key feature of the Sashimi strategy is that it only allows eliminations within the group of the odd-out cell. In this case, it would be the central group containing the digit 2 highlighted in orange.
 
This technique is a process sliced into two assumptions:
 
1. There are only two possibilities for number 2 in the second row. If the digit in orange is true, then the candidates circled in red are not possible. Nor is the other 2 in the same row.

2. Assuming that the cell in yellow has the number 2 as a candidate, there would be a Finned Swordfish pattern on the grid. The 2 in orange would be the fin. By applying that technique, the candidates circled in red would not be possible. (Remember the Sashimi only applies to groups).
 
Conclusion: based on these two assumptions, the candidates circled in red would be impossible in both cases. According to the Sashimi technique, they can be safely eliminated.
  

 
The Sudoku Swordfish strategy is one of the most recurrent in the advanced levels of these puzzles. In theory, it should be applied only in the later stages of the game. As there are fewer candidates per cell, the likelihood of this strategy resulting in the solution for one or more cells increases.
However, as the player will find out with practice, the pattern required to apply it rarely occurs in the early stages of the game anyway.