6 Advanced Sudoku Strategies explained

Advanced Sudoku strategies are used in the hardest levels of these puzzles and they can either help to reduce candidates or find the solution for a specific cell. Regardless, their application always demands high levels of concentration from the player as they work by deduction.

1. The X-Wing

The X-Wing method is one of the most basic advanced Sudoku strategies. It can also be applied at some intermediate levels, although its incidence is very low in these cases. Its goal is to eliminate candidates.

The player can use this strategy when there is one candidate repeated in four cells that form a square or rectangle when mentally connected by row and column. By making an X linking diagonally the two opposite corners of this rectangle, the player finds only two possible sets of positions for that digit.

The next step will be to test those sets on the grid and eliminate the digit from any cell that would become impossible in both situations.

Example

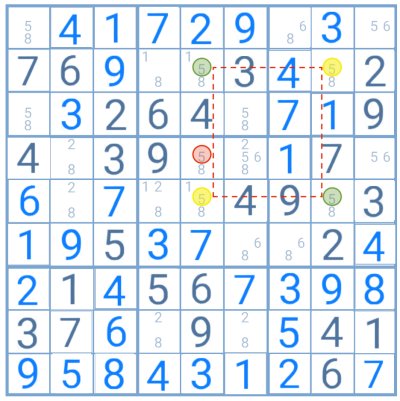
In this example, the number 5 forms the necessary pattern to apply the X-Wing strategy. By connecting the cells containing it, it is easy to see that in this situation only the pairs in green or yellow could be possible. Testing the pairs on the grid shows that the 5 highlighted in red would be impossible in both cases. It can then be eliminated as a candidate for that cell. 

2. The Swordfish

This strategy helps to eliminate a candidate from cells as well. To apply it, the player must find a digit candidate for two cells in the same row, in three different rows. These cells must also be aligned by column, regardless of the shape they create.

Connecting them will result in a closed chain that reveals two sets of possible placements for that digit. The player can then put them to the test and eliminate that number as a candidate to the cells where it would become impossible in both cases.

Example

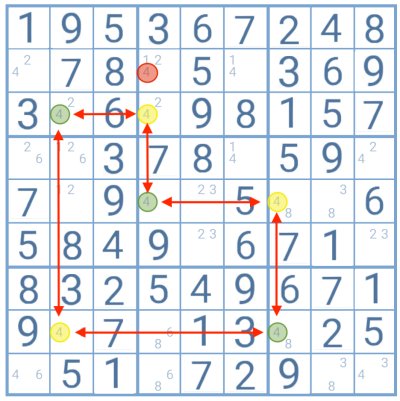
In this grid, number 4 is a candidate for two cells in three different rows, allowing the player to use the Swordfish technique.

Connecting them reveals that whenever a digit highlighted in green is possible, the yellows become impossible, and vice-versa. Thus, there are only two sets of possibilities within this chain for number 4, the green and the yellow sets.

When testing them on the grid, the player finds that the 4 highlighted in red would be an impossible candidate in both cases. It can then be safely removed from that cell, leaving only numbers 1 and 2 as candidates for it.

3. Forcing Chains

Forcing chains are one of the easiest advanced Sudoku strategies to understand. Unfortunately, applying it requires very high levels of concentration and the outcome can be uncertain. When it does work, it gives the player the solution for one cell.

To apply a simple forcing chain, there must be cells with only two candidates in the grid. The player picks one and begins testing the changes to the puzzle when applying each of the two digits in that cell. The goal is to find if there is a cell that would bear the same result whichever digit is used. If so, that will safely be the solution for it.

Example

In this example, the top highlighted cell with the candidates 1 and 2 was used to apply the forcing chains technique. When testing for both digits, the player finds that the outcome for the highlighted cell with candidates 5 and 7 is always 5. Therefore, this digit will be the solution for that particular cell.

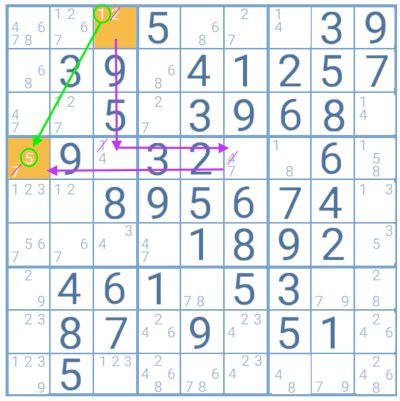
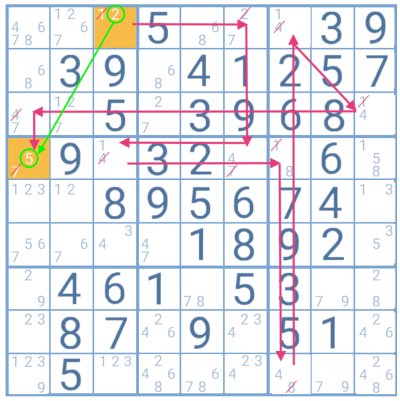
Note that when testing for number 1, the player could also have made a chain by going right (to the cell with 1 and 4 as candidates). The chain would be longer, but the result is the same. Then number 5 is still the answer to the highlighted cell.

Out of the advanced Sudoku strategies, the forcing chains method is usually a last resort as the chains can be very long and complicated and they do not always produce results.

4. The XY-Wing

The XY-Wing is a strategy to remove candidates. It can be applied when there are three cells in the grid, each with only a pair of candidates that share at least one digit among them (e.g. AB/AC/CB). With a bit of mental effort, the player can picture a Y when connecting them, with one cell working as the stem and the remaining as the branches.

The next step is to trace lines in each row and column of the cells to form a square or rectangle. If any of the shared digits are candidates within the lines connecting the cells or at an intersection point, they can be safely removed.

Example

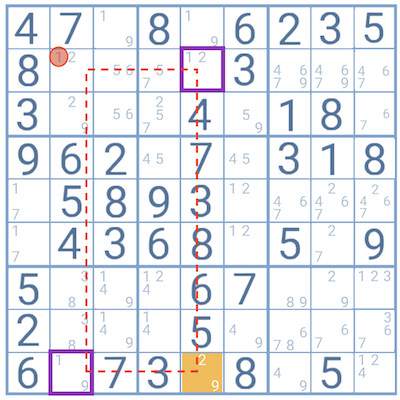
In the example above, the stem cell contains the digits 2 and 9 (highlighted in orange) and connects to the branches, each with one of these digits as candidates (purple squares).

If any of the cells on the red paths contained one candidate shared by the cells on the extremities of the lines, it could be eliminated, but this is not the case.

However, the cell at the intersection of both branches of the Y contains a shared digit between both (number 1), allowing the player to eliminate it as a candidate for that cell.

5. Unique Rectangle Type 1

Any Sudoku puzzle must have only one possible solution. However, at the most extreme levels, the players might find themselves with two. This happens when there is a “deadly pattern”. This pattern happens when there are 4 cells with the same pair of candidates facing each other. For it to be “deadly” each set of two cells must also be placed within the same group.

To avoid having multiple solutions, the player must apply the strategy of the unique rectangle. During the game, and when facing the prospect of a deadly pattern, the player must check if one of those four cells has any other candidates in them. If so, the player can eliminate the problematic digits from it and leave the remaining candidates.

Example

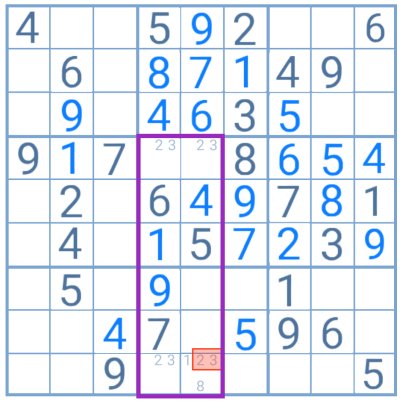
In this example, the player faces a possible deadly pattern with the candidates 2 and 3, in which the placement of those digits can become indifferent in the end and result in two possible solutions for the puzzle. Since one of the cells also contains 8 as a candidate, the player can use the unique rectangle method to eliminate the pair 2 and 3 from it and avoid the deadly pattern in the end.

In theory, the unique rectangle technique should be the least used out of the advanced Sudoku strategies, even in the hardest levels, as this pattern only occurs when the puzzle is poorly designed albeit not wrong.

6. Nishio

The Nishio strategy takes its name from professional puzzle player Tetsuya Nishio who is credited with inventing it. Out of all the advanced Sudoku strategies, this is the one that players avoid the most and use only as a last resort as it takes guessing as a premise.

Basically, the player must take a cell with two candidates, choose one, and try to solve the grid. If it works, great. If not, the player must return to the starting point and choose the other. The point of this strategy is that as soon as an incompatibility arises, the starting candidate can be eliminated which turns the remaining one into the solution for that cell.

However, a simple miscalculation due to lack of concentration can turn the puzzle unsolvable, and/or the incompatibility might not arise until the very end of the puzzle, which is why players tend to avoid this technique.
 
 
The theoretical approach of advanced Sudoku strategies is relatively easy to understand and apply. The biggest difficulty is finding the right patterns on the grid and knowing which technique to use in each case.

Nevertheless, only experts reach the levels in which they are required and at that point knowing and being familiar with these strategies becomes a requirement to progress in the hardest levels of these puzzles.