The 45-rule in Sudoku: what is it and how to apply it
The 45-rule is one of the most basic Sudoku strategies but its usefulness and importance in solving Killer Sudoku puzzles cannot be overstated. While in classic puzzles it is merely a matter of common sense and a natural consequence of the rules, in the Killer variant it becomes essential to solve any grid, even those designed for beginners.
What is the 45-rule in Sudoku?
The 45-rule stems from the most basic rule of Sudoku: you must fill the grid with numbers from 1 to 9, without repeating any digits per row, column, or 3x3 group. Since there cannot be any repeated digits, the sum of each row, column, and group will always be 45 (1+2+3+4+5+6+7+8+9=45).
How to apply this strategy in classic puzzles
The rule of 45 is not very useful for solving classic Sudoku puzzles. One could even argue that it is not a strategy at all in this case, but rather a different way of understanding the dynamics of the grid.
For example, imagine that you have a partially completed grid, and row 1 is as follows: 1, 2, 3, 4, blank, 6, 7, blank, 9. You have two ways of approaching this row. The first, and most direct, is to check which numbers from 1 to 9 are missing. In this example, they are numbers 5 and 8.
The second way would be to subtract the known numbers from 45 and then try to understand how you can split the value into two cells without repeating any digit. So: 45-1-2-3-4-6-7-9=13. What combinations can you use with two numbers from 1 to 9 to reach the sum of 13 while avoiding the digits already in that row (to avoid repetitions)? Only 5 and 8.
As you can see, the 45-rule is not very useful overall in classic Sudoku puzzles. However, when it comes to the variant Killer Sudoku, things are very different.
Killer Sudoku and arithmetic
Arithmetic is fundamental to solving Killer Sudoku puzzles due to the presence of cages. These are contained groups of cells that run across the grid and always indicate the sum of the numbers within them. Following Sudoku’s logic, there cannot be any repeated digits within the cages, regardless of the position of their cells within the grid.
These cages provide important clues about the position of the numbers, which is why Killer grids often start with fewer or even no pre-filled cells.
For example, if you have a 2-cell cage with a sum of 5 in row 1, you can reduce the candidates in those two cells to the numbers 1, 2, 3, and 4. Now let’s assume that row 1 already has a 4 in it. That cage could only contain the naked pair 3/2 in that case. Using arithmetic and a single cell with the number 4, you have the solution to 3 out of 9 cells in that row, even if you are not yet sure of the exact order of the numbers in the cage.
To help you progress smoothly through the grid, prepare a pen and paper or use an online calculator.
How to apply the 45-rule in Killer Sudoku
The 45-rule revolves around the sum of the digits in a given row, column, or group. Provided there are no repetitions, the order of the digits is irrelevant. When you combine this idea with that of cages, you get a powerful strategy to solve any Killer Sudoku.
The premise is simple. When you have several cages contained within a row, column, or group, you can subtract their sum from the total of 45. The result will be the value of the cells lying outside those cages. This strategy can either reduce the number of candidates in those cells or help you find the solution to them.
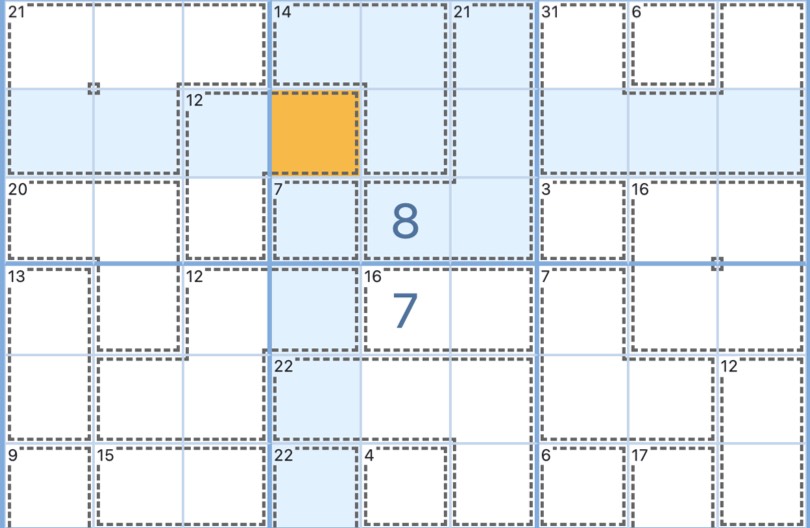
Example 1: 3x3 group
In this example, we find three cages fully contained within the 3x3 group in the top left corner (24, 17, 3). The selected cell, however, belongs to a cage that crosses over to a different group. Let’s apply the 45-rule to the contained cages: 45-24-17-3=1. The solution for the selected cell is 1.
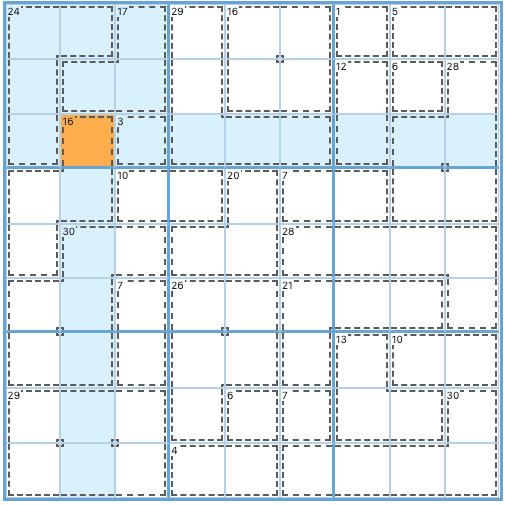
Example 2: row
In this example, row 2 has two contained cages (14+14) and two cells belonging to cages that cross to other rows. You can ignore the numbers inside the contained cages because they are irrelevant to the 45-rule. It’s the sum of the cages that is important. Let’s start there: 45-14-14=17.
Now you know that the combined value of the two outlier cells is 17. Since one of these cells already has a 9 in it, you can find the solution for the highlighted cell in R2C5: 17-9=8.
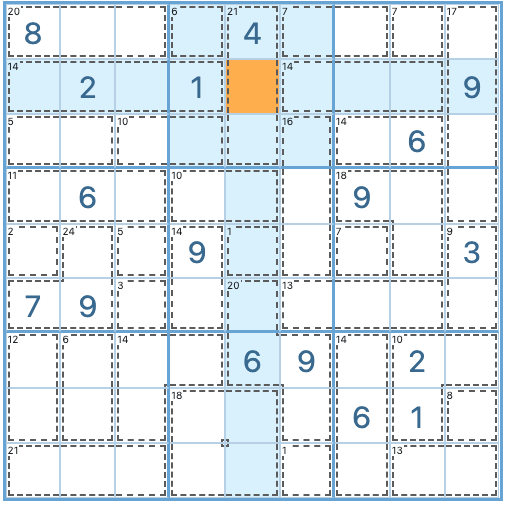
Using the 45-rule to reduce candidates
The examples above illustrate cases where the conditions to apply the 45-rule in Killer Sudoku puzzles were perfectly met. Unfortunately, these cases are the exception when it comes to hard and evil puzzles. In those, the 45-rule tends to become a strategy to reduce candidates rather than one to solve cells.
Let’s go back to Example 2. In it, you have two outlier cells. You only know that cell R2C5 contains an 8 because cell R2C9 already has a 9 in it. Otherwise, you would only know the sum of the two: 17. In other words, even without knowing their solution, you could reduce the candidates for both outlier cells. In this case, there is only one way of reaching the sum of 17 by combining two numbers from 1 to 9: the naked pair 8/9.
Example 3: reducing candidates
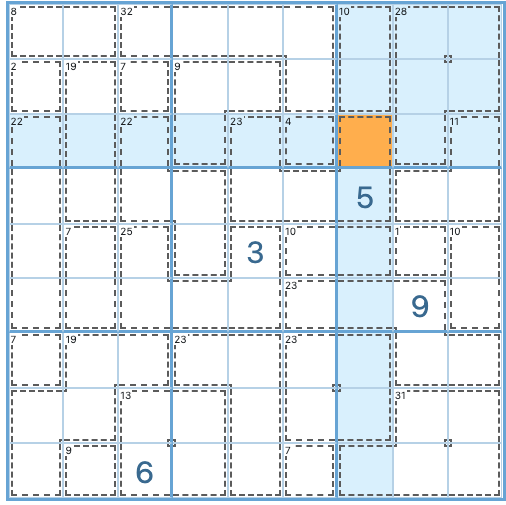
In the grid above, the 3x3 group in the top right corner has two contained cages (28 and 10) and two outlier cells. Let’s apply the 45-rule to the contained cages: 45-28-10=7
Now we know that the sum of the two outlier cells is 7, but not the solution for each one. There are three possible combinations (1+6=7, 2+5=7, and 3+4=7), which translates into 6 candidates for each cell. But stay positive: without knowing the solution for any of the cells in that group or row 3, we eliminated three candidates (7, 8, 9)!
Despite being a beginner’s strategy, the 45-rule in Sudoku is one of the most useful tools to solve the hard-locked grids of Killer Sudoku. Not only that, but it is also a promoter of the many benefits of Sudoku since it triggers more logical reasoning and thinking from the players, who will also have to brush up on their addition and subtraction skills along with probabilities. Start applying this strategy now, and soon enough you will master any Killer Sudoku grid!












