Sudoku X-Wing technique: when and how to use

The Sudoku X-Wing strategy is one of the most frequent techniques that can be applied to Sudoku puzzles from a medium difficulty level onwards. It is a very straightforward technique with an easily identifiable pattern. It focuses on one single digit and its goal is to restrict the number of cells that can have that number as a possible candidate.
 
Together with the Swordfish, the Sudoku-X-Wing technique is also a valuable strategy for any player to learn as it branches out into more complex patterns and techniques that are required to solve impossible puzzles.

Requirements to apply the Sudoku X-Wing strategy

To be able to apply this technique, the player must find 2 rows or 2 columns where a single digit is a candidate for only two cells of each. These cells must be aligned by column and row, forming a square or rectangle when connected.
 
The basic principle of this technique is simple. Since the digit has only two possible solutions in the rows or columns under analysis and each cell is directly affected by the others, the player can identify only two possible sets of solutions for the digit. That is, the pairs formed by the cells diagonally opposite to one another.
 
By testing each set of possibilities on the grid, it becomes clear that whenever the Sudoku X-Wing technique is applied to rows, the digit under analysis cannot be a candidate for any cell in the columns connected to the base cells. Likewise, with X-Wing patterns on columns, it is impossible for the digit to be a candidate in the rows connected to the base pattern.

Practical example

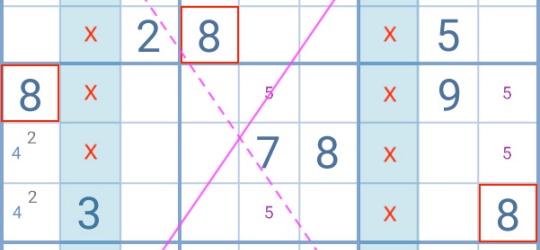
According to the basic rules of Sudoku, every row and column must contain the numbers from 1 to 9 without repetitions.
 
In the example above, it is clear that the number 8 has only two possible solutions within the highlighted columns. Since these 4 cells are aligned by column and row, it is possible to apply the Sudoku X-Wing technique.
 
If the two 8 connected by the dotted line are true, the other pair becomes false and vice-versa. Trying both configurations reveals that, regardless of the final answer, the number 8 cannot be a candidate in the rows connecting to the base pattern. Thus, the 8 circled in red between the two highlighted yellow cells at the bottom can be eliminated.

Finned X-Wing

Throughout the puzzle, it is usual for the player to find incomplete Sudoku X-Wing patterns. Sometimes, one of the vertices of the rectangle/square is missing because the digit is a candidate for more cells in that row/column and the 2 by 2 requirement of the X-Wing pattern is not met.
 
However, when the extra possibilities for the digit are restricted to one group, the player has a Finned X-Wing pattern. The fins, in this case, will be the extra positions for the digit.

The player must then ask themselves:
1. If either of the fins is true, which candidates can I eliminate?
2. If the fins are false, the X-Wing pattern applies. Which candidates can I eliminate then?
 
The candidates that become impossible when answering both questions, can be safely removed.

Practical example

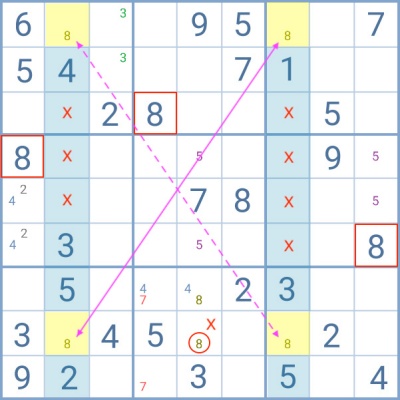
In this example, the player would have a typical Sudoku X-Wing row pattern if the cells highlighted in orange did not have the number 5 as a candidate. Since they do, one of the requirements to apply this technique is not met.
 
However, it is possible to use the Finned strategy, since the orange cells, or fins, are restricted to one group.
 
The players must then ask themselves:
1. If the solution for number 5 lies in one of the orange cells, which candidates can I eliminate?
2. And what if the regular X-Wing pattern applies?
 
In this case, only the 5 circled in red would be eliminated when answering both questions.

Sashimi X-Wing

The Sashimi pattern is very similar to the traditional Sudoku X-Wing configuration. In this case, the player also finds one digit with only two possible solutions within two rows/columns.
 
Yet, one of the cells is not connected to another by row or column. As a result, the connection between these cells results in a crooked rectangle or square.
 
As with the Sudoku X-Wing, the player should then take each pair of digits diagonally opposite to each other and test them on the grid. The candidates that become impossible with both sets, can be eliminated.

Practical example

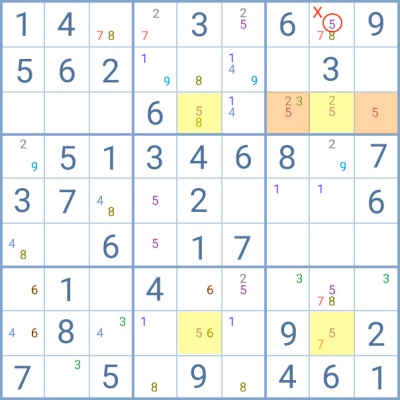
Looking at this grid, the player finds two columns with only two possibilities each for number 3. While the cells highlighted in yellow seem to form an X-Wing pattern, the cell in orange prevents the formation of a perfect rectangle since it is not aligned by row.  
 
However, the basic principle of an X-Wing still applies, because number 3 has only two possible solutions in each column. Since the two bottom cells are connected, the relations within the pattern work just the same as with a typical X-Wing, with two sets of possible solutions.
 
The main difference is that the player cannot immediately eliminate the 3s from the rows connecting to the base pattern. With the Sashimi technique, there is no shortcut. It is necessary to test both sets on the grid.
 
In this example, the 3 circled in red become impossible when both sets are applied, except for the one in row 2, column 7, which is the solution for that group. All the others can safely be eliminated.

 
The Sudoku X-Wing pattern is so common that the player may find several simultaneously during a game. They can be formed by different digits or by the same digit positioned in different rows or columns.

As long as the requirements for the use of this technique are met by each of the patterns, the player can apply it to all of them and thus reduce the number of candidates present on the grid even more.