Sudoku Unique Rectangle: Types and Patterns

The Unique Rectangle set of strategies comprises useful techniques that are relevant throughout all the difficulty levels of Sudoku. In easier puzzles, these strategies have a high chance of revealing the solution for one or more cells, while in harder levels they can either provide a solution or help to reduce the number of candidates in several cells.
 
This set of strategies assumes that Sudoku puzzles cannot have more than one solution. Thus, when facing a disposition that may potentially lead to multiple solutions, they reveal the only possible course of action.

Unique Rectangle Type 1

This strategy applies when the player finds four cells with the same pair of candidates facing each other. They are grouped in parallel sets of two, sharing the same columns, rows, and blocks. This is a deadly pattern that results in a double solution for the puzzle.
 
However, a well-designed grid will always ensure that an extra candidate is also possible in at least one of the cells of the rectangle. This number is necessary to break the deadly pattern and it is the solution to that cell.

Example

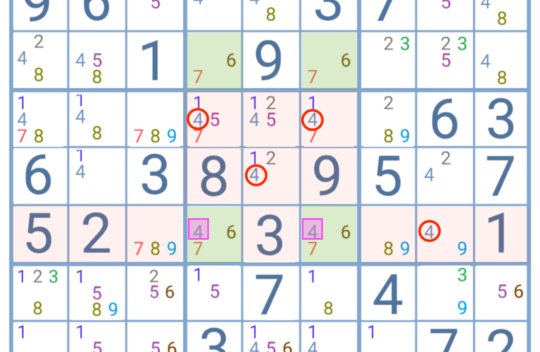
In this example, the four cells containing the pair 2/3 form a unique rectangle as they are not affected by any other cell in the grid. Thus, they could potentially create a double solution situation as the position of the 2 or the 3 is indifferent.
 
Nevertheless, one of the cells in this rectangle has two extra candidates, the 1 and the 8. These digits will break the deadly pattern. The numbers 2 and 3 can be eliminated as candidates for that cell.

Unique Rectangle Type 2

The Type 2 strategy follows the same assumptions as Type 1, but instead of providing a solution, it helps to reduce the number of candidates.
 
In this pattern, the player finds the same setting as before, but now two cells contain the same extra candidate. If these cells share the same row, column, and/or group, it is possible to remove the digit as a candidate to any other cell in those areas.

Example

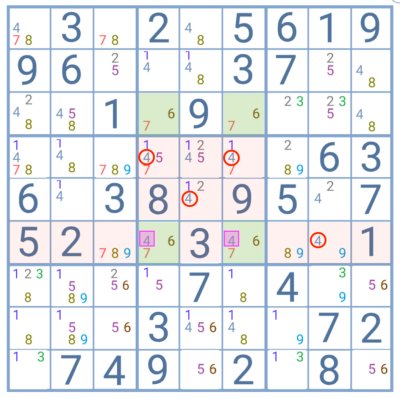
Numbers 7 and 6 form the deadly pattern in this puzzle, with number 4 working as the extra digit. As this digit will have to break the pattern, the player knows for certain that its solution is within those 2 cells. Therefore, it cannot be a candidate for any other cell within that group or row. The digits circled in red can be eliminated.

Unique Rectangle Type 3

This technique combines the basic rectangular pattern with the concept of locked subsets. As with Type 2, two aligned cells of the pattern contain extra candidates but now these digits are not similar. Yet, those cells will be for certain the solution to one of them.
 
The player must then search for a cell that contains only the pair of pattern breakers as candidates. It must also be connected to the base cells. When available, it is possible to eliminate the pattern breakers as candidates to other cells in the areas shared by the pattern and that specific cell.

Example

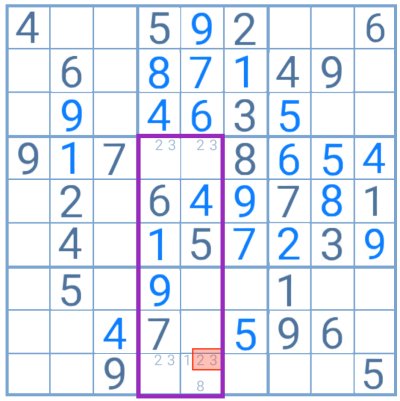
The numbers 3 and 8 are the pattern breakers in this example. The player knows that either one or the other will be positioned in one of those two cells.
 
In their column, there is also a cell containing only this pair as candidates (highlighted in orange). Thus, if the 3 is the pattern breaker the solution to the orange cell will be 8. If 8 is the pattern breaker then its solution will be the 3.
 
In short, the player knows for sure the 8 and the 3 will be positioned in one of those three cells. They can then be eliminated from the remaining cells in that same column.

Unique Rectangle Type 4

The Type 4 technique is only a variation of Type 2. A combination of the two strategies is also possible.
 
As with Type 2, the player finds the same pattern breaker in two different cells that share a column or row, but in the Type 4 technique, these also need to share the same block.
 
The player knows that these two cells will be filled with the extra candidate plus one of the digits of the deadly pattern. If out of the base pair, one digit is not a candidate to any other cell within that row, column, or block, then the second digit of the pair becomes invalid in those two cells.

Example

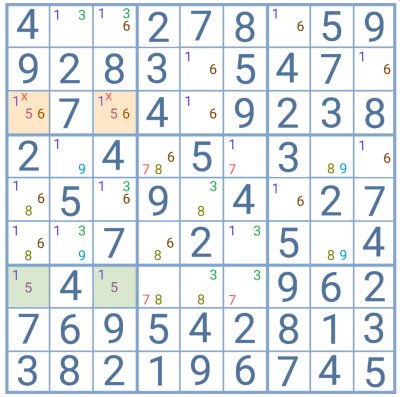
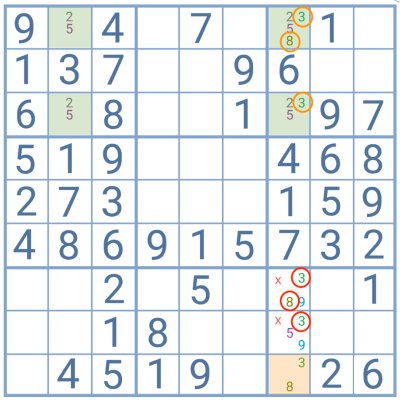
In this example, the pair 1/5 forms the deadly pattern while the 6 works as the pattern breaker.
 
The player knows that one orange cell will contain a 6 while the other will be either a 1 or a 5. However, the 5 is not a candidate for any other position within that block. This means that the orange cells contain a hidden naked pair formed by the 6 and the 5. The 1 can thus be removed as a candidate for either of them.

Unique Rectangle Type 5

With this strategy, the player finds two or three cells with the same pattern breaker but these are not necessarily connected by row, column, and/or block. However, it is still possible to remove it as a candidate for all the cells that are simultaneously affected by those cells in the pattern.

Example

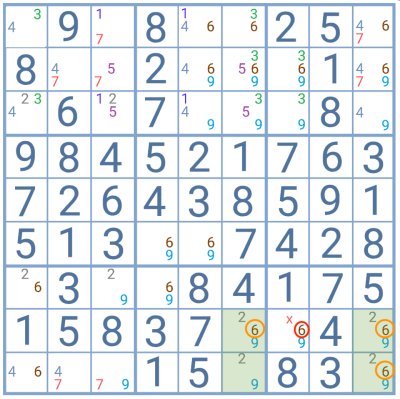
Three cells contain the number 6 as the pattern breaker in this example. One of these will have to be the solution for 6. Therefore, this digit can be eliminated as a candidate for any cell affected simultaneously by the three cells.
 
 
 
The Unique Rectangle set of strategies is very useful to progress at any Sudoku difficulty level. It is also one of the most used by players as it is easy to identify the required pattern to apply any of its techniques.